Tag Archives for pythagorean theorem
rotatable draggable MCs
2007Click and drag the polaroid to move it, click and drag a corner to rotate it.
| High Strung – Photo courtesy of Patricia Bower & Rodolfo Baras) |
DOWNLOAD SRC
1. _root Setup>
On the _root level we have a polaroid of the band High Strung, which we want the user to be able to move & rotate. In the .fla, the name of this movieclip is "polaroid." Also on the _root level is a small transparent movieclip, called "mouseTarget" which will assist in the rotation functions.
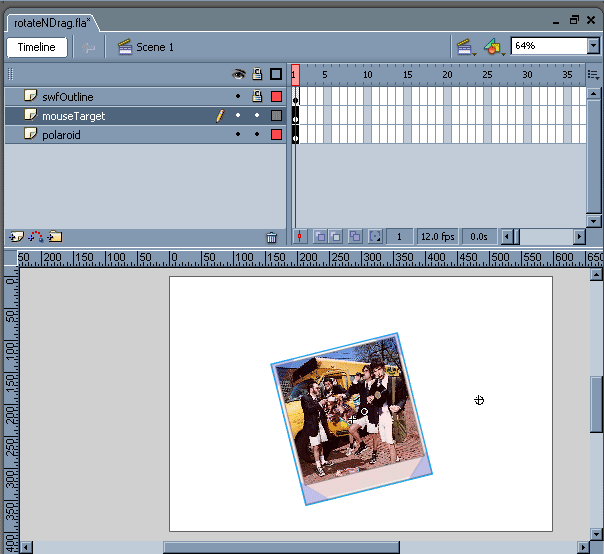
2. polaroid>
Within the "polaroid" mc is the mc "dragElements" which contains the Actionscript and Shapes used for ‘hotspots.’ If you’ve multiple objects you want the user to drag and rotate, simply duplicate this clip and place it within each MC on the top layer & level.
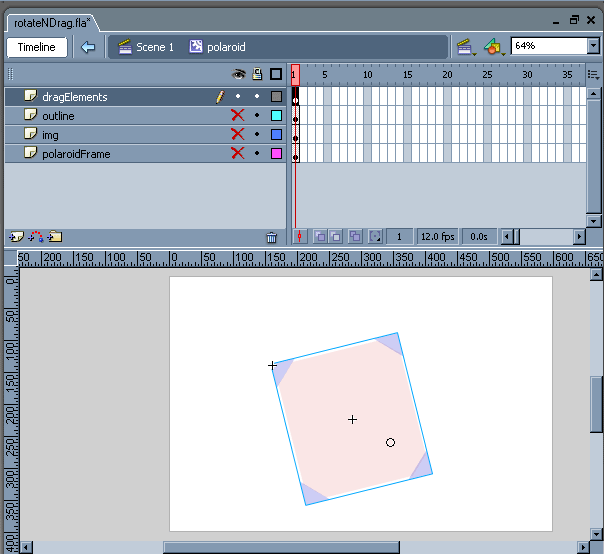
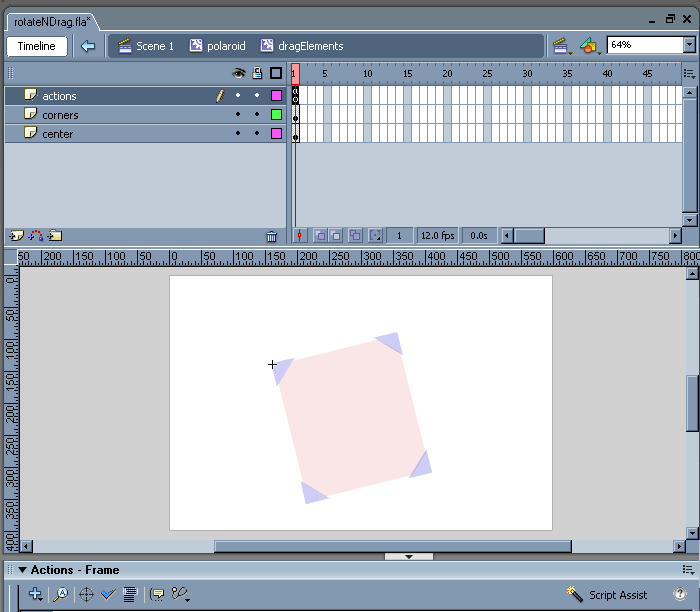
There are plenty of ways one can approach defining one’s interactive areas; in this case. when the user clicks and drags the corner shapes, which are contained within their own MC, the rotating functions will be called. When they click and drag over the central square, they’ll be able to drag the polaroid about on the stage with a startDrag().
Below right is an explanation of the Functions.
 |
|||||||||||||||||||||||||||
|
Dragging A typical startDrag(), but because the object can be rotated, its absolute width and height are constantly changing, which is why the startDrag limits must be defined each onPress() Rotating In order to rotate the object based on the user’s cursor movement, we need to find the starting angle between the cursor and object origin when the user first clicks, and then calculate the change in that angle as the user moves the cursor clockwise or counter-clockwise. This is accomplished with the function getCurrentAngle(). Dust off your trig
Because the difference in x and y provide us with the opposite and adjacent legs, we’ll go with an inverse tangent function.
getEdges() The edges of the parent object change with rotation, so to keep it within the borders of the stage this function will be used in a couple places to grab the x & y values of those edges. Start Rotating! When the user rolls over the corners, a startDrag() is applied to the the mouseTarget mc on the _root level, who’s x & y location will be used in the getCurrentAngle() function. When pressed, the initial angle from cursor to center is calculated with getCurrentAngle(), and an onEnterFrame is set up to do so continuously, then rotate the object appropriately based on the difference, while ensuring with a conditional statement that the objects edges are within the boundaries of the initially defined stage. onRelease, the onEnterFrame is nullified, and a new one set up to take care of any remaining overlap (in case the user yanks a corner of the object to outside of the stage limits and lets go of the mouse). onRollout, the mouseTarget on the _root.level no longer gets dragged, until the user rolls over another corner. |
wrapping dynamic text to a curve
Short and sweet, but I’ve seen it come up on a couple of projects to stump others and myself. And really, it’s not that daunting when armed with a few right triangles and the good ol’ Pythagorean theorum.
DOWNLOAD SRC
If you want to wrap a block of text to a curve, this isn’t quite the tutorial you’re looking for, though the same principles apply – you’ll have to figure out the maximum width of each line, split the copy into an array, and loop through it creating textfields and checking their textWidth to determine where the linebreaks should occur. Additionally, you might also check out gskinner’s textflowpro.
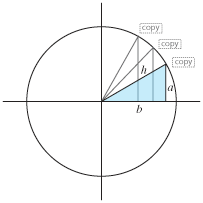 The trick is thinking of the curve as part of a circle, and then looking at the x/y location of the TextField or Object as 2 legs of a triangle whose hypotenuse is the radius of that circle.
The trick is thinking of the curve as part of a circle, and then looking at the x/y location of the TextField or Object as 2 legs of a triangle whose hypotenuse is the radius of that circle. Which means that if we know the radius to be a constant, and we know the y-location which presumably updates incrementally, then we can easily solve for the x-location using:
a2 + b 2 = h2
∴
b = √h2 – a 2
import gs.TweenLite;
var list:Array = new Array("alpha", "bravo", "charlie", "delta", "echo", "foxtrot", "golf", "hotel", "india", "juliet", "kilo", "lima", "mike", "november", "oscar", "papa", "quebec", "romeo", "sierra", "tango", "uniform", "whiskey", "x-ray", "yankee", "zulu");
var curveCategories:Array = new Array();
var textForm = new TextFormat;
textForm.font = "Helvetica";
textForm.size = 10;
textForm.align = "left";
textForm.color = 0x777777;
//set init location vars
var xLoc : Number = 0;
var yLoc : Number = 15;
var yIncrement : Number = 17;
for (var i : Number = 0; i < list.length; i++) {
//create textfield
curveCategories[i] = new TextField;
curveCategories[i].htmlText = list[i];
curveCategories[i].embedFonts = true;
curveCategories[i].autoSize = "left";
curveCategories[i].setTextFormat(textForm);
//calculate x based on y and radius of circle
var r : Number = 250;
var originY : Number = 260;
var originX : Number = 20;
var legVert : Number = Math.round(Math.sqrt(Math.pow(originY – yLoc, 2)));
var legHoriz : Number = Math.round(Math.sqrt(Math.pow(r, 2) – Math.pow(legVert, 2)) + originX);
curveCategories[i].y = yLoc;
curveCategories[i].x = legHoriz;
curveCategories[i].alpha = 1;
//update y
yLoc += yIncrement;
//animate/add to stage
TweenLite.from(curveCategories[i], .4, {alpha:0, x:legHoriz+30, delay:.1 * i});
addChild(curveCategories[i]);
}
var list:Array = new Array("alpha", "bravo", "charlie", "delta", "echo", "foxtrot", "golf", "hotel", "india", "juliet", "kilo", "lima", "mike", "november", "oscar", "papa", "quebec", "romeo", "sierra", "tango", "uniform", "whiskey", "x-ray", "yankee", "zulu");
var curveCategories:Array = new Array();
var textForm = new TextFormat;
textForm.font = "Helvetica";
textForm.size = 10;
textForm.align = "left";
textForm.color = 0x777777;
//set init location vars
var xLoc : Number = 0;
var yLoc : Number = 15;
var yIncrement : Number = 17;
for (var i : Number = 0; i < list.length; i++) {
//create textfield
curveCategories[i] = new TextField;
curveCategories[i].htmlText = list[i];
curveCategories[i].embedFonts = true;
curveCategories[i].autoSize = "left";
curveCategories[i].setTextFormat(textForm);
//calculate x based on y and radius of circle
var r : Number = 250;
var originY : Number = 260;
var originX : Number = 20;
var legVert : Number = Math.round(Math.sqrt(Math.pow(originY – yLoc, 2)));
var legHoriz : Number = Math.round(Math.sqrt(Math.pow(r, 2) – Math.pow(legVert, 2)) + originX);
curveCategories[i].y = yLoc;
curveCategories[i].x = legHoriz;
curveCategories[i].alpha = 1;
//update y
yLoc += yIncrement;
//animate/add to stage
TweenLite.from(curveCategories[i], .4, {alpha:0, x:legHoriz+30, delay:.1 * i});
addChild(curveCategories[i]);
}
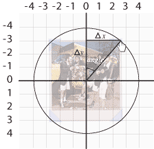 If
the angle we’re trying to define can be considered
1 of the non-right angles in a right triangle, we
can use the difference in x and y to find its value.
The change in x & y are initially set to positive
in getCurrentAngle() for the purpose of the equation.
If
the angle we’re trying to define can be considered
1 of the non-right angles in a right triangle, we
can use the difference in x and y to find its value.
The change in x & y are initially set to positive
in getCurrentAngle() for the purpose of the equation.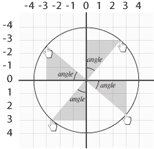 Knowing which value to plug into the opposite or
adjacent variables is dependent on which quadrant
the triangle resides. There are 4 quadrants, thus
4 possible orientations of this triangle, thus 4
conditional cases in the function determined by
the positivity or negativity of the change in x
or y. The result is converted from radians to degrees
(1 radian = 57.2957795 degrees) before the appropriate
multiple of 90 is added to get the total rotation.
Knowing which value to plug into the opposite or
adjacent variables is dependent on which quadrant
the triangle resides. There are 4 quadrants, thus
4 possible orientations of this triangle, thus 4
conditional cases in the function determined by
the positivity or negativity of the change in x
or y. The result is converted from radians to degrees
(1 radian = 57.2957795 degrees) before the appropriate
multiple of 90 is added to get the total rotation.